Ресурсы для изучения математики
•
Александр Котов
•
1084 слов
математика
образование
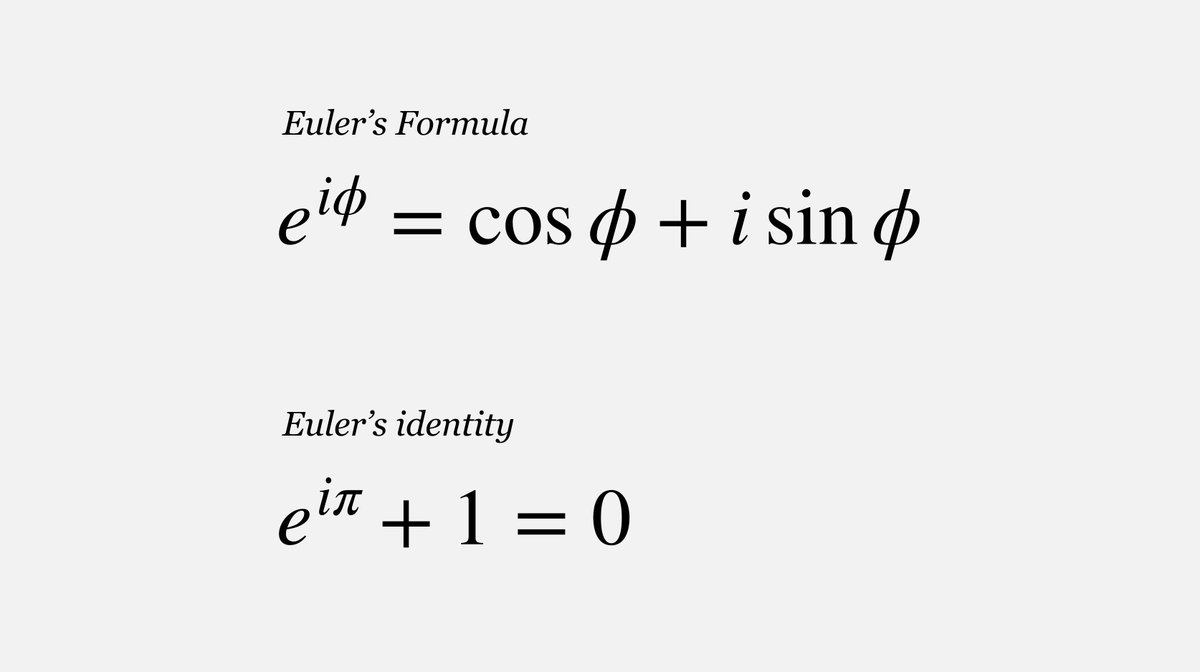
Без математики невозможно представить себе информатику. Не считая некоторых междисциплинарных разделов, компьютерную науку можно считать частью математики. Работа любого программиста, веб-разработчика и даже системного администратора требует понимания не только школьной математики, но также как минимум логики, теории множеств и комбинаторики, которые изучаются в школе далеко не всегда. О сложности создания каких-то инновационных технологий, что нас только и интересует, и говорить не приходится. В наше время программистами часто становятся люди без высшего профессионального образования. Недостаток знаний может быть очень неприятным обстоятельством, мешающим достижению целей. Поэтому мы подготовили список ресурсов, которые помогут в изучении математики. Учёбу в вузе это, скорее всего, не заменит, но будет очень полезно.
Все ресурсы в данной статье разделены на несколько категорий в зависимости от формата. Внутри категории мы постарались разместить их в порядке возрастания сложности. При этом материалы на одну тему из разных категорий желательно изучать одновременно для лучшего понимания. Например, можно одновременно читать книгу, слушать лекции и решать задачи.
Темы выбраны в зависимости от интересов и потребностей автора статьи, то есть примерно со старших классов школы до начальных курсов вуза. Если вам это не подходит, то можете поискать более простые или более сложные материалы в тех же источниках.
Если что-то не понятно с первого раза, не отчаивайтесь. Просто пробуйте снова и снова, изучайте по другим источникам. Профессор Санкт-Петербургского государственного университета Николай Вавилов в одной из лекций представленного здесь курса лекций по высшей алгебре описал процесс обучения математике так: «Нужно учиться математике как маленькие дети учатся языку. Детям не объясняют каждое слово, им говорят: «Вот, смотри, это факторкольцо» или «Это коцикл»».
После долгой подготовки этой статьи мы понимаем, что далеко не всё, что хотелось бы видеть в ней, было включено. Подготовка материалов занимает много времени. Однако мы хотим поделиться тем, что имеется, уже сейчас. В будущем мы постараемся выпустить новую версию, в которой будет ещё больше материалов.
Khan Academy
Платформа Khan Academy[1] целиком ориентирована на практику. Далеко не все используемые теоремы строго доказываются, а смысл приёмов не всегда объясняется подробно. Зато здесь можно хорошо отточить навыки, а объяснения очень доступны даже тем, кто не обладает хорошим знанием теории.
Платформа поддерживает только английский язык. Для тех, кто владеет техническим английским, это не будет помехой, однако в некоторых заданиях нужна повышенная внимательность, поскольку ответ зависит от словесной формулировки задачи.
- Algebra 2[2] — многочлены, комплексные числа, показательные уравнения, логарифмы, трансформации функций, тригонометрия.
- Trigonometry[3] — небольшой курс по тригонометрии.
- Precalculus[4] — комплексные числа, многочлены, бином Ньютона, тригонометрия, векторы, матрицы, числовые последовательности, конические сечения, комбинаторика и теория вероятностей.
- Statistics and Probability[5] — подробный курс по теории вероятностей, математической статистике и дизайну исследований.
Coursera
Платформа Coursera[6] позволяет прослушать курс, который может состоять из лекций и текстовых материалов, сдать тесты и получить сертификат. Сами материалы доступны бесплатно, однако для получения сертификата, а зачастую и для сдачи тестов, придётся заплатить за каждый курс по 2167 рублей на момент написания статьи. Мы не уверены в том, что это является полезным вложением, но материалы могут быть полезны как дополнительный источник информации по указанным темам, если практические задания вы решаете из другого источника, как рекомендуется в начале статьи.
Мы выбирали только курсы на русском языке. Выбор среди курсов на английском может быть гораздо разнообразнее, рекомендуем поискать самостоятельно.
- Математика для всех[7] — отличный курс при участии Алексея Савватеева позволяет развить математическую интуицию, применимую в самых разных практических задачах.
- Комбинаторика для начинающих[8] — доступное объяснение основ комбинатории при участии Андрея Райгородского.
- Теория вероятностей для начинающих[9] — доступное объяснение основ теории вероятностей при участии Андрея Райгородского.
Курсы лекций
Такой формат, как курс лекций, не заменяет ни практических занятий в плане получения навыков, ни книг в плане строгости и систематизированности теории. Однако он служит отличным дополнением и к тому, и к другому. Особым преимуществом этого формата являются активное участие и творческая свобода лектора, что позволяет ему в полной мере использовать свой преподавательский талант и акцентировать внимание на самых важных и интересных моментах. Поэтому мы крайне рекомендуем представленные курсы лекций.
- Математический анализ[10] — повторение школьного математического анализа от Бориса Трушина.
- Математическая логика[11] — язык и теоремы математической логики, исчисление высказываний и предикатов, немного философии, истории логики и формализации математики.
- Теория групп[12] — небольшой курс Алексея Савватеева по теории групп, доступный даже для школьников.
- Линейная алгебра[13] — основы линейной алгебры от 3Blue1Brown в переводе на русский язык.
- Алгебра и геометрия[14] — векторы, матрицы, базисы, системы линейный уравнений, многочлены, векторные пространства, группы, кольца, поля.
- Высшая алгебра[15] — упоминавшийся в начале статьи курс по высшей алгебре от Николая Вавилова.
- Статистика[16] — курс от Бориса Бояршинова по статистике, в основном по практическому применению математической статистики и дизайну исследований.
Видеоканалы
Хотя некоторые материалы из этих каналов были включены в данную статью, в них можно найти ещё много чего интересного.
- Борис Трушин[17]
- Маткульт-привет! :: Алексей Савватеев и Ко[18]
- 3Blue1Brown[19]
- 3Blue1Brown Русский[20]
- Wild Mathing[21]
- Лекторий ФПМИ[22]
- Лекториум[23]
Лекции и занятия
Представленные здесь видео помогут вспомнить школьные темы, раскроют их подробнее и помогут установить связь между простейшими понятиями математики и высшей математикой. Автор почти всех видео — Борис Трушин.
- Квадратный трёхчлен
- Бином Ньютона[28]
- Треугольник Паскаля[29]
- Как возводить в иррациональную степень[30]
- Про степень с действительным показателем[31]
- Комплексные числа
- Как повернуть параболу (и гиперболу)[35]
- Введение в математический анализ[36] (до 1:17:30)
Литература
В представленный список литературы входят как учебники, так и сборники задач. Учебники незаменимы в плане полноты и строгости изложения, а сборники задач гораздо обширнее, чем предложенные в статье курсы с практикой.
- Виленкин Н. Я. Комбинаторика — М.: Наука, 1969 — 328 c.
- Генкин С. А., Итенберг И. В., Фомин Д. В. Ленинградские математические кружки — Киров: АСА, 1994 — 272 c. — ISBN 5-87400-072-0
- Архипов Г. И., Садовничий В. А., Чубариков В. Н. Лекции по математическому анализу — М.: Высшая школа, 1999 — 695 c. — ISBN 5-06-003596-4
- Зорич В. А. Математический анализ. Часть I — 6-е изд. — М.: МЦНМО, 2012 — 702 c. — ISBN 978-5-94057-891-8
- Зорич В. Ф. Математический анализ. Часть II — 6-е изд. — М.: МЦНМО, 2021 — 818 c. — ISBN 978-5-94057-893-2
- Демидович Б. П. Сборник задач и упражнений по математическому анализу — М.: АСТ, 2005 — 558 c. — ISBN 5-17-010062-0
- Кремер Н. Ш. Теория вероятностей и математическая статистика — 3-е изд. — М.: ЮНИТИ-ДАНА, 2010 — 551 с. — ISBN 978-5-238-01270-4
- Кострикин А. И. Введение в алгебру. Часть I. Основы алгебры — 3-е изд. — М.: ФИЗМАТЛИТ, 2004 — 272 с. — ISBN 5-9221-0487-Х
- Кострикин А. И. Введение в алгебру. Часть II. Линейная алгебра — М.: Физико-математическая литература, 2000 — 368 с. — ISBN 5-9221-0018-1
- Кострикин А. И. Введение в алгебру. Часть III. Основные структуры — 3-е изд. — М.: ФИЗМАТЛИТ, 2004 — 272 с. — ISBN 5-9221-0489-6
- Винберг Э. Б. Курс алгебры. — 2-е изд. — М.: Факториал Пресс, 2001 — 544 с.
- Сборник задач по алгебре под редакцией А. И. Кострикина — 3-е изд. — М.: ФИЗМАТЛИТ, 2001 — 464 c. — ISBN 5-9221-0020-3
Ссылки
- Khan Academy
- Khan Academy: Algebra 2
- Khan Academy: Trigonometry
- Khan Academy: Precalculus
- Khan Academy: Statistics and Probability
- Coursera — Learn new job skills in online courses from industry leaders like Google, IBM, & Meta. Advance your career with top degrees from Michigan, Penn, Imperial & more.
- Coursera: Математика для всех
- Coursera: Комбинаторика для начинающих
- Coursera: Теория вероятностей для начинающих
- Математический анализ
- Математическая логика
- Теория групп — Курс из 8 лекций по основам теории групп для школьников и студентов, прочитанный Алексеем Савватеевым
- Линейная алгебра
- Алгебра и геометрия
- Высшая алгебра
- Статистика
- Борис Трушин — Личный канал преподавателя математики онлайн-школы «Фоксфорд» Бориса Трушина
- Маткульт-привет! :: Алексей Савватеев и Ко
- 3Blue1Brown — Some combination of math and entertainment, depending on your disposition
- 3Blue1Brown Русский — Комбинация математики и развлечения, в зависимости от Вашего настроения
- Wild Mathing
- Лекторий ФПМИ
- Лекториум — Платформа открытых знаний
- Квадратный трёхчлен #1 | Формула для корней и теорема Виета
- Квадратный трёхчлен #2 | Парабола
- Квадратный трёхчлен #3 | Квадратные неравенства
- Квадратный трёхчлен #4 | Уравнения, сводящиеся к квадратным
- Бином Ньютона
- Треугольник Паскаля
- Как возводить в иррациональную степень
- Про степень с действительным показателем
- Комплексные числа. Введение
- Комплексные числа. Тригонометрическая форма. Формула Муавра
- Комплексные числа. Комплексная степень
- Как повернуть параболу (и гиперболу)
- Введение в математический анализ